Logic Chapter Seventeen
Next Chapter

Associativity Laws, and Exam Preparation

To get ready for the midterm, you can download Exam Preparation Sheet
To help with remembering the rules, download Rules Sheet

Now here's some more theorems that definitely need DML!

I mean, they're obviously true, but how to prove them? Well, here's the first one.

1.   2. 3. 4.  5. 6. 7. 8. 9. 10. 11. 12.     Show   P v (Q v R) (P v Q) v R P v (Q v R) Show   (P v Q) v R ~ [(P v Q) v R] ~ (P v Q) ^ ~ R ~ (P v Q) ~ P ^ ~Q ~ P Q v R ~Q R ~ R CP  ACP  IP  AIP  4, DML 5, S 6, DML 7, S 2, 8, DS 7, S 9, 10, DS 5, S

Can you figure out how to prove the other three? Well number 12 should be about the same as number 11, but what about numbers 13 and 14?

Actually, numbers 13 and 14 are incredibly easy! Think about it. If you have trouble with them, see the hint at the bottom of this page.

For practice, and to prepare for the quiz, here are some arguments. Identify and cross out the invalid ones. circle and derive the valid ones. (Use the truth table method to determine validity, if needed.)

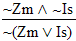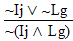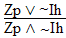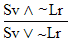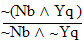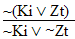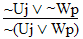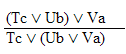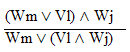practice 17. Use your own paper or the answer sheet at logic12homework.rtf. For each of the following arguments do TWO things. First,circle it if it's valid, cross it out if it's invalid. 1. 2. 3. 4. 5. 6. 7. 8.   Second, Prove all the valid ones.

To get ready for the midterm, you can download Exam Preparation Sheet
To help with remembering the rules, download Rules Sheet

Hint for theorems 13 and 14: Use S and CJ.

Copyright © 2005 by Martin C. Young

Next Chapter

---

This Site is Proudly Hosted By: