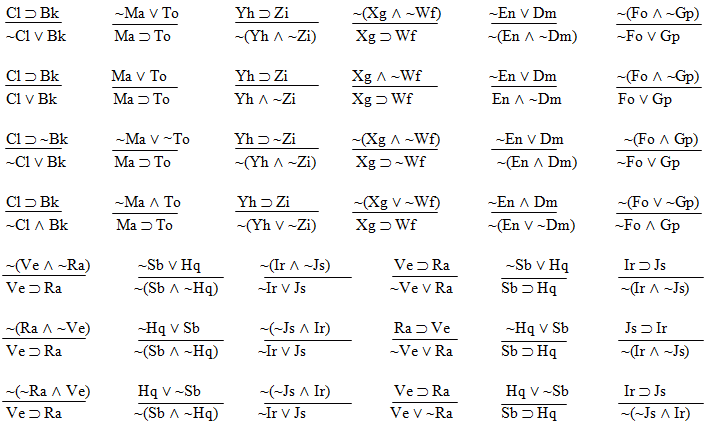Logic Chapter Sixteen
Next Chapter

Deriving De Morgan's Laws, . . . um, well, maybe not.

Here's those theorems again.

Theorems 5 & 6 (De Morgan's Laws) 
3. ~(P ^ Q) (~P v ~Q)
4. ~(P v Q) (~P ^ ~Q)


Notice that De Morgan's Laws can't get you from ~(R ^ S) to ~R ^ ~S. Those two sentences are not logically equivalent to each other.
Neither are ~(R v S) and ~R v ~S or ~(R ^ S) and ~(R v S).
The only two logical equivalences we have are (~R v ~S) ~(R ^ S) and ~(R v S) (~R ^ ~S)

Okay, so here's the derivation for one of De Morgan's laws.

Oh Gawd! What was I thinking? This thing's a monster! What will I do?

I know! I'll make De Morgan's Laws a rule, so no-one will have to prove them!

Rule 18: De Morgan's Laws (DML) Comes in four little rules.
1. If "~(R ^ S)" is an available line, then "~R v ~S" may be written as a new line in the derivation, and
2. If "~(R v S)" is an available line, then "~R ^ ~S" may be written as a new line in the derivation, and
3. If "~R v ~S" is an available line, then "~(R ^ S)" may be written as a new line in the derivation, and
4. If "~R ^ ~S" is an available line, then "~(R v S)" may be written as a new line in the derivation.

What do you think? Is there any logical reason why DML can't be both a rule and a set of theorems?

Notice the following facts about applications of DML to placeholders like "S" and "R"..
1. If we start with one tilde ("~"), we end up with two.
2. If we start with two tildes, we end up with one.
3. If we start with a carat ("^"), we end up with a wedge ("v").
4. If we start with a wedge, we end up with a carat.
5. If we start without parentheses, we end up with them.
6. If we start with parentheses, we end up without them.

We need DML to prove things like two out of the following four theorems.



As I shall now demonstrate. (Notice that only one of these uses DML. Why is that?
1.
2.
3.
4.
5.
6.
7.
8.
Show (O P) (~O v P)
O P 
Show   ~O v P
~ (~O v P)
~ ~ O ^ ~ P
~ P
~ O 
~ ~O 
CP
ACP
IP 
AIP
4, DML
5, S
2, 6, MT
5, S
1.
2.
3.
4.
5.
6.
7.
8.
 
 Show  (~O v P) (O P)
~O v P
Show  O P
O
Show P
~ P
~ O
O
CP 1.
ACP2.
CP3.
AIP4.
IP5.
AIP6.
2, 6, DS7.
4, R8.
Can you figure out how to prove the other two theorems?

For practice, and to prepare for the quiz, here are some arguments. Identify and cross out the invalid ones. circle and derive the valid ones. (Use the truth table method to determine validity, if needed.)





Copyright © 2005 by Martin C. Young

Next Chapter
This Site is Proudly Hosted By:
WEBster Computing Services