
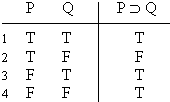
|
|
||||||||
|
|
||||||||
|
|
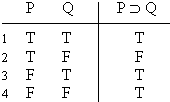
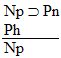
|
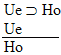
|
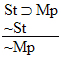
|
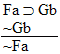
|
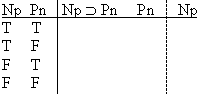
|

|
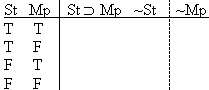
|
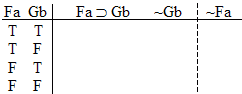
|
| If
NASA sent an expedition to Mars and back in 1974 then we'd have Mars
rocks on Earth. We do have Mars rocks on Earth. (This is true!) So NASA did send an expedition to Mars and back in 1974. |
| If saboteurs from Luxembourg had planted a nuclear device in Mount Saint Helens, that mountain would have blown up. Mount Saint Helens did blow up, so Luxembourg did sent saboteurs to the US. |
| If the British had caught and executed Benjamin Franklin in 1777, Benjamin Franklin would be dead. Benjamin Franklin is dead, so the British did catch and execute Benjamin Franklin in 1777. |
| If NASA sent an expedition to Mars and back in 1974 then we'd have Mars rocks on Earth. NASA didn't send an expedition to Mars and back in 1974, so there are no Mars rocks on Earth. |
| If saboteurs from Luxembourg had planted a nuclear device in Mount Saint Helens, that mountain would have blown up. Luxembourg has never sent saboteurs to the US, so Mount Saint Helens has never blown up. |
| If the British had caught and executed Benjamin Franklin in 1777, Benjamin Franklin would be dead. The British did not catch and execute Benjamin Franklin in 1777, so Benjamin Franklin is not dead. |
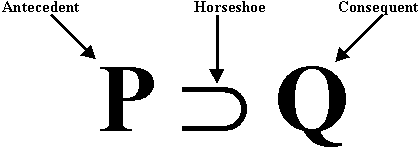
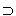 Q means IF the antecedent, (P) is true, then the consequent (Q) is true. Which means that if we want to prove a conditional statement, all we have to prove is that IF we assume that the antecedent is true THEN the consequent will be true. So lets have a rule that lets us make
that assumption that the antecedent is true, and which agrees that, if
we've proved the consequent, then we've proved the whole conditional.
Q means IF the antecedent, (P) is true, then the consequent (Q) is true. Which means that if we want to prove a conditional statement, all we have to prove is that IF we assume that the antecedent is true THEN the consequent will be true. So lets have a rule that lets us make
that assumption that the antecedent is true, and which agrees that, if
we've proved the consequent, then we've proved the whole conditional. | Rule 10. Conditional Proof (Abbreviated by "CP") IF, and ONLY IF, you first write a show line of "Show P 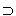 Q" you may write "P" as the next line, justifying it by "ACP," for "Assumption for Conditional Proof." Q" you may write "P" as the next line, justifying it by "ACP," for "Assumption for Conditional Proof."IF, and ONLY IF, you subsequently produce "Q" as an available line, and there is no other uncancelled "show" between that show line and that "Q", then that "show" may be cancelled, and a box may be drawn around that formula and any other lines there may be between it and it's show line. If the relevant show line is line #1, then the derivation is successfully finished. (Write "CP" by the show line.) (Rules 7-13 are conveniently listed on Logic Rules Sheet Two ) |


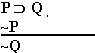 Is it valid or not? Well, what do you think?
Is it valid or not? Well, what do you think? 
| Rule 11. Repetition (Abbreviated by "R") If "P" appears as an available line, then "P" may be written as a new line. (Rules 7-13 are conveniently listed on Logic Rules Sheet Two ) |
 |
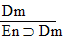 |
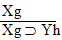 |
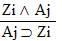 |
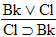 |
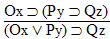 |
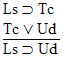 |
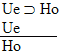 |
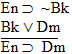 |
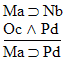 |
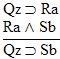 |
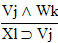 |
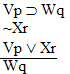 |
 |
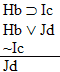 |
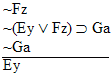 |
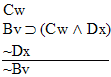 |
 |
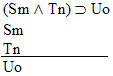 |
 |
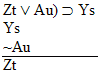 |
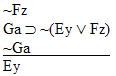 |
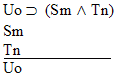 |
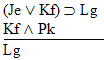 |
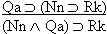 |
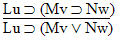 |
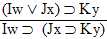 |
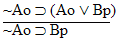 |
||
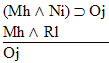 |
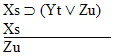 |
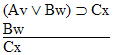 |
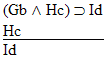 |
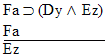 |
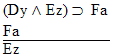 |
 |
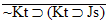 |
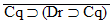 |
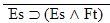 |
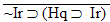 |
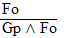 |
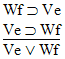 |
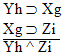 |
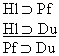 |
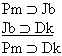 |
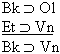 |
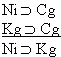 |
| Practice 10. Use your own paper or the answer sheet at practice. This practice sheet requires you to derive at least four arguments. Circle the valid arguments, and cross out the invalid ones. Try to see if you can evaluate the arguments by just looking at them and thinking about the meanings of the formulas. Then check your answers, and evaluate the other arguments, by truth table. Finally, indentify the arguments that can be derived by conditional Proof, and derive them.
|
