Mike is insane
Ossie is hairy
No-one is green
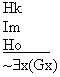
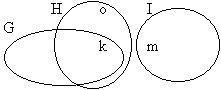
Ossie is green
Everything is green
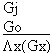
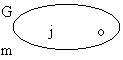
| Keith is hairy Mike is insane Ossie is hairy No-one is green |
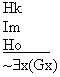 |
is proved invalid by | 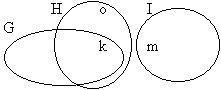 |
| Jeff is green Ossie is green Everything is green |
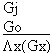 |
is proved invalid by | 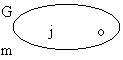 |
| Jeff is not a kangaroo A kangaroo exists |
|
is proved invalid by |
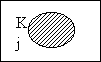 |
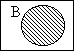
| Nigel is an elk A non-elk exists |
|
is proved invalid by |
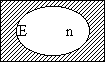 |
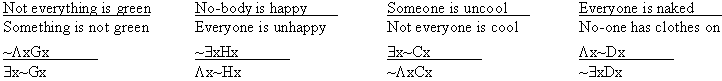
 |
Is Is ~ |
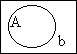 |
Is Is ~ |
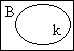 |
Is Is ~ |
 |
Is Is ~ |
 |
Is ~ Is |
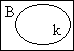 |
Is ~ Is |
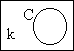 |
Is ~ Is |
 |
Is ~ Is |
| Practice 12. Use your own paper or the answer sheet at Practice Sheet. For each of the following arguments do TWO things. First, translate it into English based on the following scheme.
Second, circle it if it's valid, cross it out if it's invalid.
|
