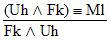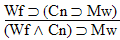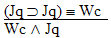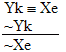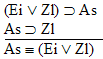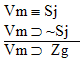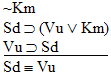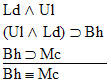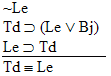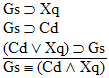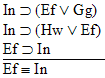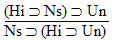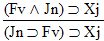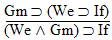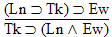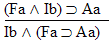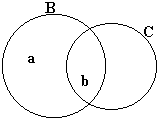
Ba |
Bb |
|
Ba |
Bb |
|
Ca |
Bb |
|
Ba |
Bb |
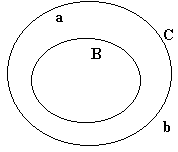
|
Ba |
Bb |
|
Ba |
Bb |
|
Ca |
Bb |
|
Ba |
Bb |
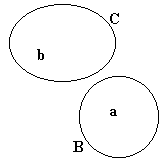
|
Ba |
Bb |
|
Ba |
Bb |
|
Ca |
Bb |
|
Ba |
Bb |
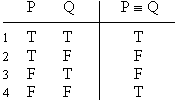
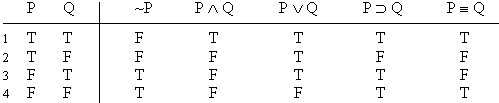
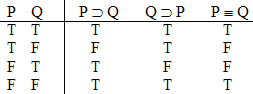
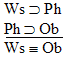
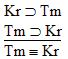
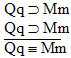
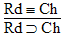
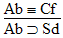
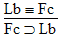
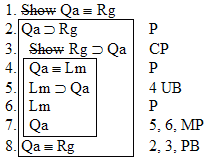
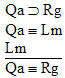 is a
valid argument, and here's the proof:
is a
valid argument, and here's the proof: