Logic Chapter Six

Logic Chapter Six
Next Chapter

DERIVATIONS

A "derivation" is a particular kind of proof. Derivations are more complicated than pictures because there's all these rules you have to know. And most of these rules have some kind of weird trick to them. Okay, each individual rule is pretty simple when you get to know it, but you have to be careful because they're all very different from each other, and you have to follow each of them exactly.

We're all used to rules that tell us what we can't do. These rules tell us what we can do. Everything else is forbidden. If there isn't a rule saying explicitly that you can do it, then you can't do it. You can only do what the rules say you can.

We start a derivation by writing the number "1," the word "show" and following it with the conclusion of the argument we want to prove. And maybe numbering a few more lines to get started. Say we want to prove this (really, really, really simple) argument:

We start by writing

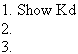
Before we go on, I want to point out a few things. The word "show" is there to indicate that we want to prove Kd, but we haven't proved it yet. That means we can't do anything with Kd. If the word "show" wasn't there, Kd would be available to do things with, so long as it isn't in a box. (I'll explain about being in boxes later. It's not important now.) Since "availability" is important, I'll put it in a definition:

An available line is a line in the derivation that does not have an uncancelled "show" in front of it, and is not currently inside a box. Only whole lines can be available. Parts of lines are never available.

Remember, line one above is not available.

Basically, you can write the word "show" followed by any formula you like at any time. However, writing the wrong "show" line can make your derivation impossible to finish!

Now we need rules to allow us to do things inside derivations. Since a premise is something that is taken as true by the argument, (it may or may not be true in real life) we should be able to write down premises. So:

Rule 1. Premise (Abbreviated by "P")
If "P" is a premise of the argument being derived, then "P" may be written as a new line in the derivation.
(The first six rules are conveniently listed on Logic Rules Sheet One)

New lines are always written in by the very next free number. Given this rule, we can add to our derivation.

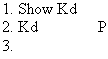
The rule "premise" allows us to write down Kd, because it's a premise. We write "P" off to the side to remind us which rule we used. But wait! Kd is also what we're trying to show here! So we've done it. All we need now is a rule that lets us show that we've finished.

Rule 2. Box and Cancel (Direct Proof)
If the formula indicated by "show" appears as an available line below that show line, and there is no other uncancelled "show" between that show line and that formula, then that "show" may be cancelled, and a box may be drawn around that formula and any other lines there may be between it and it's show line. If the relevant show line is line #1, then the derivation is successfully finished.
(The first six rules are conveniently listed on Logic Rules Sheet One)

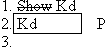
Since Kd on line 2 is not already in a box, and doesn't have an uncancelled "show" in front of it, we can box and cancel.

And we're done! (Since we don't need line 3, we can ignore it.)

I want to emphasize, as clearly as I can, that derivations only prove validity. A successful derivation does not prove that the argument has a true conclusion. All it proves is a sort of conditional, "what-if" kind of fact. A successful derivation proves that if (and that's a big if) all the premises are true, then (and only then) the conclusion cannot be false. Again, it does not prove that the conclusion is true, it just proves the logical relationship between the premises and the conclusion. It's a very important relationship, which is why it has its own special name, but it's just a logical relationship.

Rule 3. Conjunction (Abbreviated by "CJ")
If "P" and "Q" are both available lines, they can be joined together by putting a " ^ " between them to make a new sentence "P ^ Q" which may be written as a new line in the derivation.
(The first six rules are conveniently listed on Logic Rules Sheet One)

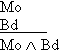Let's say we want to prove we could do it as follows

Notice that we start by writing "show" and the argument's conclusion. Then we write the premises one at a time. Next we apply rule 3, which gives us our conclusion, and finally, because we have that conclusion, we can box and cancel.

Test yourself. Is there another way we could have derived that argument? (Using only lines that help us.) Well, there's a way that's slightly different. Click here if you know the answer. (The hint is that rule P allows us to write the premises in any way we like, and rule CJ allows us to use any two available lines.)

One more rule

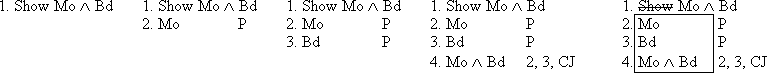
Rule 4. Simplification (Abbreviated by "S")
If "P ^ Q" is an available line, then either "P" or "Q" may be written as a new line in the derivation.
(The first six rules are conveniently listed on Logic Rules Sheet One)

Now here's a fairly complicated argument.

Okay, it looks simple. But how do we deal with all those brackets? Like this:

This might look like it's way too complicated, but every single step is necessary. Remember, only whole lines can be available, so we can't take terms out of the premise and put them together again without breaking that premise down line by line. Sure, the premise and the conclusion say exactly the same thing. But they don't say it he same way, and we can only make moves that are allowed by the rules. So no shortcuts, no skipped steps.

Now test yourself. Derive each of the following arguments. (Beware! Not all of them are valid.) Once you've worked out the answer for youself, (no peeking), check your answer by clicking on the relevant argument. If you think the argument has something wrong with it, click on it to check what that is.

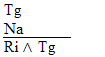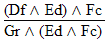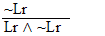
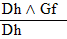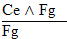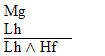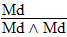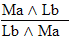Practice 6. Use your own paper or the answer sheet at practice 06. For each of the following arguments, determine whether it is valid or invalid. If it's valid prove it valid by DERIVATION. If it's invalid prove it invalid by venn diagram or truth table.

1.	Ug Tf ^ Ug
2.	Af ^ Bg
3.	Ch ^ Di Di ^ Ch
4.	Ej ^ Fk Fk ^ Gl

This Site is Proudly Hosted By: