
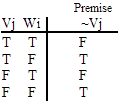


| Ta ^ ~Wb | Tg v~Wh | (Tn ^ Vn) ^ Um | Ve ^ (Ud v Wc) | (Tf v Ue) v Wd | ((Tm ^ Ul) v Vj) ^ Wi |
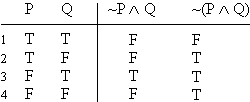
| ~Vc ^ Vd | ~Ui v Uj | Wl ^ (Tj ^ Vi) | (Wm v Vl) ^ Wj | Tc v (Ub v Va) | Th v (Ug ^ (Vf v We)) |
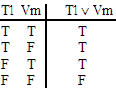
| ~ (Te ^ Wf ) | ~ (Tl v Vm) | (Uh ^ Vg) v Uf | Ti v (Vh ^ Wg) | (Tb ^ Ua) v (Un ^ Wn) | (Td v Uc) ^ (Vb v Wa) |
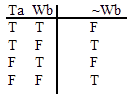
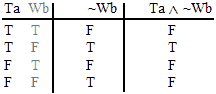
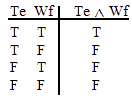
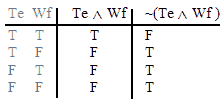
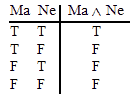
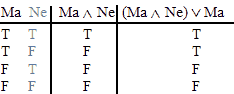
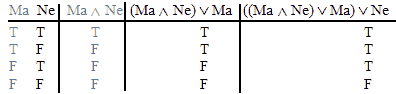

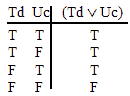 and
and
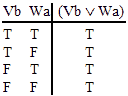

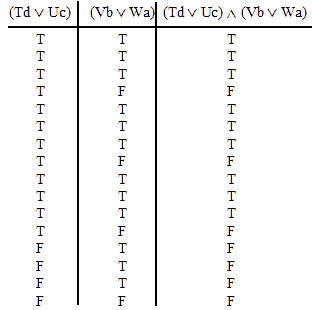

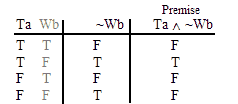
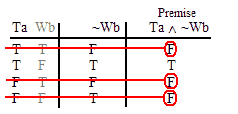
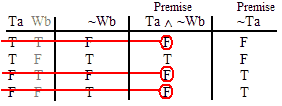
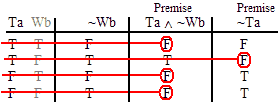 VALID.
VALID.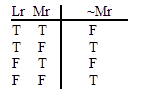
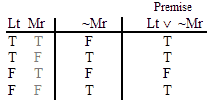
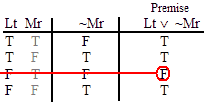
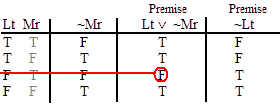
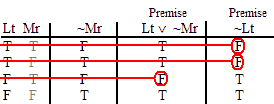
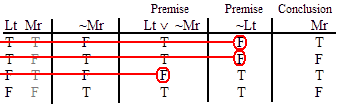
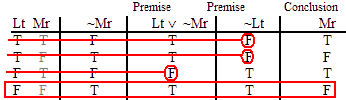 INVALID (by line 4.)
INVALID (by line 4.)
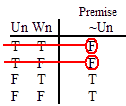
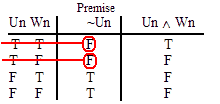
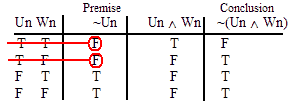
 VALID.
VALID. |
 |
 |
 |
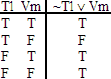 |
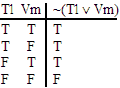 |
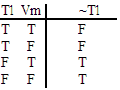 |
 |
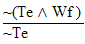 |
 |
 |
 |
 |
 |
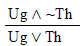 |
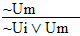 |
practice 5. Use your own paper or the answer
sheet at practice.
For each of the
following arguments, prove it valid or invalid by truth table.
|
