Introduction To Sampling Arguments

For the purposes of this course, the word "argument" will be used to refer to any attempt to persuade another person that some claim is or is not true. This chapter will teach the basic analysis of a special kind of argument I call a "sampling argument." Sampling arguments are commonly used to support general statements. Generalizations are statements that cover the whole of some population, such as Americans, wombats, the water in the oceans, left-handed Armenian mole-diggers, Scotsmen with Irish names, tea-drinkers, trees, people who do horrible things to turnips... well, you get the idea. A sampling argument is an argument that starts with a "sample," a small group of taken by some method from a larger population, and then attempts to persuade us that a feature clearly seen in the sample must therefore also be a feature of the population.

Main Topic: Sampling

The essence of a sampling argument is the "sample." Usually, populations are so large that we cannot reasonably test the state of every member of that population. For instance, if we wanted to know what proportion of Scotsmen get tipsy (slightly drunk) on Hogmanay, we cannot possibly hire enough obervers to follow around every Scotsman around on the evening of December 31st. (Especially if we count female Scots as "Scotsmen" Oh, lets just call them "Scots."), so we're scre... I mean, so we have to fall back on looking at a much smaller number of Scots and extrapolating the results to all haggis-eatin', kilt-wearin' caber-tossers. (This is perhaps an unfair characterization of the Scots. Very few of them actually toss cabers.) So let's just hire people to follow around a randomly selected group of one million Scots next Hogmanay and to report on whether or not they get tipsy. Say that 75% of these randomly selected Scots get tipsy on Hogmanay, we could then make the following argument.

Exactly 75% of our sample got tipsy this Hogmanay, therefore 75% of all haggis-eaters got tipsy this Hogmanay.

Here's how the terminology of generalization matches up with this argument.

Facts
Population: All Scots (several million of them.)
Sample: One million randomly selected Scots.
Feature being tested: Tipsiness.
State of the sample: 75% tipsy at this Hogmanay.

Conclusion drawn from those facts
State of the population : 75% tipsy at this Hogmanay.

This is how a generalization works, if it works at all. A sample is taken, and it is argued that the state of the sample must be the same as the state of the population. If the state of the sample cannot reasonably be explained without assuming that the population has the same state, the argument is good. If we can reasonably explain the state of the sample without assuming that the population has the same state, the argument is no good, lousy, bogus, wack, heinous.... I'll stop now.

For another example, imagine that two people, call them "Jeeves" and "Wooster," are trying to figure out the overall composition of the following population. Imagine also that neither of them can see the population the way you can. (You can see that this population is extremely well mixed. In fact, there are only two deviations from perfect mixing. They appear in the top left and bottom right corners of the field. By some strange coincidence, that's where Jeeves and Wooster take their samples from.) They know that it's composed of 2,600 colored dots, but that's about it. Neither of them has any idea of how the dots are distributed, or anything else besides the fact that it's made up of dots. And of course, neither of them knows that the population is made up of 650 red dots (25%), 650 blue dots (25%) and 1,300 green dots (50%) Now Jeeves takes a sample from the top left corner of the population (red line) while Wooster takes a sample from the bottom right corner, (blue line). Each of them then makes a claim about the composition of the population based on their samples.

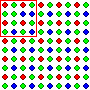
Jeeves's sample is 50% green, 25% red and 25% blue. So he claims that the population is 50% green, 25% red and 25% blue.
Wooster's sample is 25% green, 25% red and 50% blue. So he claims that the population is 25% green, 25% red and 50% blue.
That's quite a big difference. Who's closer to being right and why?

The reason Jeeves's argument is better than Wooster's argument is that argument Jeeves's sample is big enough to swallow it's imperfection in the mixing of the population (which means that his sample is representative of the population) while Wooster's sample is so small that it's imperfection crosses the sample border, distorting the result (which means that his sample isn't representative of the population). Are these samples too small? Well that depends on what we know about the structure of the population.

Sample Size

We saw above that it's possible to have a sample that's way too small to accurately represent the population it's taken from. However, it is sometimes the case that a population is structured in such a way that even a small sample can be perfectly representative, if it's taken the right way. A population is not always arranged as a chaotic mixture of individuals. Some populations are arranged in such a manner that we can take a very small sample with absolute confidence that the result will perfectly represent the composition of the population. 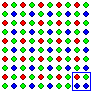For instance, consider the population of dots shown below. Imagine that we know that the population is structured in the way shown, but we don't know the colors of any of the rows. Now imagine we take the very, very, very, very small sample of exactly four dots comprising the first dot in each of the first four rows, as shown in the top left corner of the image. That's a sample of four out of four thousand. That's one per thousand, which means one tenth of one percent, or 0.001. Is that too small?

Our sample comes out 50 percent red, 25 percent blue and 25 percent green. Given that we know the structure of the population, what are the chances that the population is 50 percent red, 25 percent blue and 25 percent green?

Therefore, the following argument is very bad. (Technically, it commits what we call a red herring fallacy:)

It hasn't been proved that the dots in the picture above are 50% red, 25% blue and 25% green because the sample upon which that generalization is based is only 0.001 of the population, which is waaaaaaaay too small a sample.

The key fact here - the thing that makes this argument bad - is that the population is completely structured in alternating homogeneous rows of red, green, red and blue dots. It is this highly organized structure that allows a miniscule sample of just four dots to perfectly represent the composition of the whole population.

As a matter of fact, there is no limit to how proportionally small a sample can be. To see this, imagine a population of infinitely many dots, part of which is shown below. (The rest of the dots extend off your screen to the right.) This population is structured as you see here, in four rows of dots, each row being composed of dots of exactly the same color.

How big a sample do you need to tell the composition of this population? Will four dots do? It will if each of those four is the first dot in it's respective row. Now, that is an infinitesimal sample, which means it's equal to one divided by infinity, but that doesn't matter, because the population structure makes that proportionally infinitesimal sample perfectly representative of the whole.

There are two lessons here. The first is that even an infinitely small sample can be representative if it's properly taken from a population that has the right structure. The second is that it's possible to fail to convey the most important facts about this situation. To see this, think three things. First, think about a particular population that is very similar to the one pictured above. Second, think about two opposing arguments about that population. And third, think about two different critiques of the weaker of those two arguments. It is those two critiques that I want you to focus on here.

Key Fact: The population is arranged in equally-sized rows of indentically-colored dominoes.

Perfect Mixing

Another way to get an accurate result with a very small sample is if a population is perfectly mixed. Imagine another infinitely large population in which individuals are so perfectly mixed that every part of the population looks like the following picture. (Notice that this is NOT a random distribution of dot colors. It's a carefully structured distribution. A random distribution would be unevenly mixed, not smoothly mixed like this one.)

Try to find a four-square group, or a contiguous line of four dots that isn't a representative sample for this population.

Now imagine blindly picking dots from random places scattered through the population. How many would you have to pick to guarantee a representative sample? Not many!

Now imagine you work for a petroleum company. You check the composition of oil products so the company can decide how each tanker load will be processed. Your company's tankers contain a pumping system that circulates the oil between all the tanker's oil-carrying compartments. All the oil is moved and turbulance from the pumping process mixes the oil products so thoroughly that every centiliter in that tanker is absolutely identical to every other centiliter in that tanker. Given that a litre is one hundred centiliters, would one liter be a big enough sample to test the composition of the oil mixture in a tanker holding a billion liter of oil products?

The point here is that small sample size may make the sample untrustworthy, but there may be special circumstances that make this particular sample an accurate representative of the population, even though it is way smaller than we would normally accept as a good sample.

Estimating Sample Size: Variables and Values.

If 1% can be an adequate sample, 50% can be inadequate. Imagine that Noah was an educational administrator who had to rely on state grants for his funding. God issues a grant that will allow Noah collect two of every animal, but Noah's immediate superiors insist he spends half of God's money on computers. Thinking outside the box, Noah adapts to the situation by only including one of every animal. What if aliens later came across Noah's Ark bobbing on the flood waters, how big a sample would they need to accurately represent the animal passenger list? Say they picked 50% of the animals at random. Would that give an accurate picture? Would 90% be enough to give a picture that was accurate to within 1%?

When we're worrying about sample size for a perfectly random sampling method, it is sometimes useful to talk about variables and their values. Consider Noah's Ark, but this time without any middle-management between god and Noah. Noah marches on board two-by-two, one couple of each kind. In this situation, sex and species can both be considered variables, each with its own characteristic range of values. Sex is a variable with only two values, and thus a sampling argument concerning the sexes of the animals would only need a fairly small random sample. Species, on the other hand, is a variable with thousands of possible values. Given that Noah's Ark contains only two of each kind of animal, a sampling argument concerning the distribution of species on the Ark would need a sample size of considerably more than fifty percent, if it was based on a truly random sample. (A non-random sample could do it accurately at only fifty percent, if the sample was chosen in the right way.)

How big is big enough? Firstly, the issue of whether a particular sample is big enough doesn't depend on what percentage of the population is included. If the above well-mixed population was only four individuals large, only a 100% sample would be big enough! Anything less than four would leave out at least one color! If the above population was 8 individuals, a 50% sample would do. If it was 16, a 25% sample would work. If it was 32...

The minimum necessary sample size depends on the number of different relevant properties individuals can have, and on the degree of mixing in the population. In the well-mixed population above, the number of different relevant properties is four, because there are four colors, and the population is perfectly mixed. If the number of different properties was larger, or if the population was less well mixed, minimum necessary sample size would be larger.

So, there are two different things to think about when you consider the proportional size of a sample to it's population:

How large is the sample compared to the number of different relevant properties individuals in the population can have?
How is the population structured? Is it evenly or unevenly mixed? Are its members arranged in some way that so that the given sample is sure to be representative of the given population?

Finally, I have noticed that some students have a tendency to say that a sample size is too small when they cannot think of anything else to find wrong with the argument, or where the sample size is ten percent or less. Don't do this. If you cannot see any reason why this particular sample is too small for this particular population, given this particular sampling method and the structure of this particular population, then the sample size is not too small. Arguments are only bad when there are specific reasons to find them bad. Saying that the sample size is too small when you can't think of anything else is never a good idea.

Sample Age

Imagine you are an atmospheric scientist studying inertium monoxide levels in the atmosphere at various points in history. Like the rest of Earth's air, intertium monoxide does not react with any other gases in Earth's atmosphere. Say that because of the way inertium monoxide is produced and distributed, the level of inertium monoxide in Earth's atmosphere at any point on Earth is never more than ten percent more or less than the global average at that time. (If today's global average is 1%, there's nowhere on Earth where the inertium monoxide levels are lower than 0.9% or higher than 1.1%.) You recover an air sample that's been held absolutely isolated for three thousand years at the base of a really old glacier. (They can actually do this for samples that are several hundred years old.) The sample contains 10% inertium monoxide, so you can conclude that three thousand years ago, Earth's atmosphere held a global average of between 9 and 11 percent intertium monoxide.

Is the sample too old? Not if the sample was absolutely isolated! Remember, there's nothing in Earth's air that inertium can react with, so the sample can't change over time. Isolation prevents sample gasses from escaping and gasses from later atmospheres from getting in, so it can't change that way either. So, in this case, a three thousand year old sample is enough for a good generalization, provided that all the other factors are taken care of. Notice however that we can't use this sample to generalize about today's atmosphere. Atmospheres can change quite spectacularly over time. Imagine trying to generalize about the air in Los Angeles today based on an air sample taken in 1902! This is why I use the term obsolete, which means that we know that conditions have changed, so that the sample is no good anymore. A sample can be very old without being obsolete, and a sample can be obsolete without being very old at all.

Here's a real-life example. More than about 4 billion years ago, the solar system was nothing but a widely spread out mass of gas and dust particles which was slowly but surely organizing itself into bigger and bigger clumps, many of which banged into each other to make larger clumps. Our Earth was one of those lumps. While the Earth was first forming, it was hot and mostly molten, so the heavier materials gravitated to the center of the lump and the lighter materials were forced up to the surface. The heaviest materials became the Earth's core. Just before the Earth finished forming, a really big lump smashed into it hard enough to kick some of that core material up to the surface on the other side of the Earth. 4 billion years later, scientists found some of that material, figured out what it was, and used it to figure out the exact chemical composition of the Earth's core. Think about it. Not only is the few pounds of material they used a tiny, tiny sample relative to the total size of the Earth's core, that sample is 4 billion years old. However, the Earth's core has been subjected to enormous heat, pressure and mixing by convection, so it's extremely well mixed. Furthermore, there's no known substance that could turn into nickel-iron over any timescale, so we have good reason to think that the composition of that core has not changed in 4 billion years, and that the composition of the pieces of core material that the scientists used hadn't changed either. So in this case, a sample that's about as old as a sample can get on this planet turns out not too old!

Of course, saying "That generalization's no good because the sample's 4,000,000,000 years old!" is a red herring fallacy.

Key Fact: There isn't any substance out there that will turn into iron and nickel under these conditions, not even if you give it billions of years to do so.

And, conversely, having a very very recent sample does not guarantee a logically compelling argument. Some populations change very rapidly. Think about trying to do a generalization about present computer use, or present cell phone use, or home recording equipment, based on data from 1950.

There are two things to think about when you consider the age of a sample:

How quickly and in what ways do the things in this population and sample change over time? What forces bring about these changes, and how quickly or slowly do they operate?
Given the known rate of change in this kind of thing, was the sample taken recently enough that we have a reasonable guarantee that the sample is still representative of the population?

We always need to think about the age of a sample, but we can't dismiss a generalization based merely on age. If we have good reason to think that the sample hasn't changed since it was taken, and that either the population hasn't changed either, or the generalization is about what the population was like at the time the sample was taken, then the generalization is fine even if the sample is old. Some samples become obsolete very quickly, some stay good for a very long time indeed.

Randomness

People sometimes say that all samples have to be taken randomly, or they're no good. This isn't exactly true. There are circumstances where the population structure will make it possible for a small non-random sample to be much more representative than an equally sized random sample. Consider another set of dominoes, arranged in ten identically sized and colored rows so that each row is a different color from every other row. Selecting one domino from each row will give an exactly correct picture of the overall population. Selecting ten dominoes at random from the overall population has only a very, very, very small chance of getting an accurate picture because of the very, very high chance of getting two or more dominoes from the same row.

Sampling Method

A generalization can only work if it uses a sampling method that is completely independent of the feature being tested. If the sampling method is at all sensitive to that feature then it will tend to either seek out or avoid members of that population that have that feature. Either way, the result will be skewed.

Some people call this sensitivity "bias." I don't like that terminology. For one thing, "bias" has more than one meaning, and not all it's meanings have anything to do with the accuracy of generalizations. And a sampling method can be very biased while still giving a very accurate result. The thing to remember about "bias," is that it only counts if the bias is relevant to the feature being tested. If you're sample is biased, but you can show that the bias has nothing to do with the feature being tested, then that bias gives you no reason to throw out the study.

Let's go back to assessing the tipsiness of Hogmanaying Scots. Say we happen to know the names and addresses of three significant groups of Scots. We know the names and addresses of all Scottish accountants, all Scottish teetotalers, and all Scots who have been convicted of drunk driving at least three times. Say we examine every member of each group to see whether he or she got tipsy last Hogmanay. And say we got the following results.

1. 67% of all Scottish accountants got tipsy last Hogmanay.

2. 0% of all Scottish teetotalers got tipsy last Hogmanay.

3. 99% of all Scots who have been convicted of drunk driving at least three times got tipsy last Hogmanay.

These results can't all be representative of the whole Scottish population. At best, only one is right. So which of these figures is more reliable? The answer is, whichever one is least sensitive to the feature being tested. What do accountants have to do with tipsiness? Nothing that I can think of! But teetotalers are people who habitually abstain from alcoholic beverages. (Strange, but true.) So of course none of them got tipsy on Hogmanay. Are all Scots teetotalers? I don't think so! So that sample is definitely dependent on the feature being tested. On the other hand, habitual drunk drivers can be expected to drink more than regular Scots, so that sample is dependant too. (Notice that one of them is negatively dependent, in that it avoids the feature being tested, and the other is positively dependent, in that it seeks out the feature being tested.) So, since we can't find an obvious link between accountancy and tipsiness, sample number one is the only independant sample.

Key Facts

Key Fact 1. Being an accountant has nothing to do with getting tipsy. (Makes the sample good.)

Key Fact 2. Teetotallers don't drink, and this is a question of drinking behavior. (Makes the sample bad.)

Key Fact 3. Drunk drivers can be expected to be heavy drinkers, and this is a question of drinking behavior. (Makes the sample bad.)

It can be very difficult to tell whether or not a sampling method is dependent. The trick to telling whether or not a sample is dependant is to look at the way the sample was obtained. If it was obtained in a way that has nothing to do with any of the possible outcomes of the study, then it is not dependent. If, however, the method by which the sample was chosen is logically connected to the properties the sample is supposed to test for, then that's a dependency, and the argument is no good. Consider the following sampling methods.

1. Testing American reactions to the war in Iraq by mailing questionnaires to the membership of the American Pacifists Association.

2. Testing the distribution of blood types across the United States by taking blood samples from members of the Mayflower Society, a group which restricts its membership to people who have at least one direct ancestor that came over to America on the Mayflower.

3. Assessing the bodily proportions of 18th-century Americans by measuring antique clothes preserved by historical societies.

Obviously, the first sampling method is no good because (key fact) we would be taking our sample from a group that is already self-selected to be against any war. The second sampling method is also dependent because (key fact) the Mayflower passengers came from a very small region in Europe whereas the vast majority of other immigrants to the United States came from other regions, and continents, and (other key fact) blood type is very highly correlated with ancestry. Finally, there is the (key) fact that until recently, good quality clothing (the kind that is likely to be preserved) tended to be reused as long as it could be made to fit new people. Larger clothing was easier to alter than smaller sized clothing, so it tended to be reused until it wore out. Smaller sized clothes tended to be put away in the hope that someone would come along who could use them, so smaller sized clothing is much more likely to have been preserved than larger sized clothing. Therefore, the third sampling method is also dependent.

There are two different things to think about when you consider the sampling method used by a particular sampling argument:

What particular fraction of the population was picked out by this method? What are all the characteristics of this fraction?
How are the characteristics of this fraction, the fraction that was picked out to be the sample, related to the feature of the sampling argument? Does the chosen fraction have something in common with the feature cited in the conclusion, so that the sampling method is fatally dependent on that feature. Or does that fraction have nothing in common with the feature, so that the sample is safely independent of the feature.

The concepts of randomness and independence are very difficult for some people. There are those who think that nonrandomness is a kind of magic bullet that automatically kills an argument. Seeing that some sample was not taken randomly, they stop thinking and write things like "the sample was not taken randomly, so the argument is no good." Don't do this. Don't think that nonrandomness magically kills arguments. When you see that a sample is nonrandom, start thinking about the relationship between the sampling method and the feature cited in the conclusion. If they have nothing in common, the method is independent of the feature, and the nonrandomness does not matter.

Fallacy Row

Fallacies are specific things that can go wrong with arguments. I like to think of them as bad arguments that some people commonly mistake for logically compelling arguments. Here I will talk about those fallacies I think most relevant to sampling arguments. Some of them will also be important in other contexts, while others will only be important when we specifically discuss sampling. I will discuss six specific fallacies that I think are relevant here. They are Inadequate Sample, Obsolete sample, Dependent Sample, Anecdotal Evidence, Begging the Question and Red Herring.The first four are fallacies that are specific to sampling arguments, the last two are general fallacies that we will see again and again as we go on.

Inadequate sample occurs when the population clearly has not been shown to be so evenly mixed that a sample of this size can be reasonably assumed to properly represent the population. (Remember that 1% can sometimes be big enough while 90% (or more) can sometimes be too small.)

The International University on the Moon has over 20,000 students from all of Earth's 140 or so countries. I've taken an absolutely random sample of 10 students out of those 20,000, and 2 of those students were from Armenia, so we know that 20% of the students on the Moon are from Armenia.

Imagine that 143 countries are represented on the moon. In that case, a ten-student sample will miss at least 133 of those countries. This means that a sample needs to be at least 143 students to have a hope of being adequate, and we would probably want about 300 to have anything like a reasonable sample. (Key fact: There's about 140 different countries.)

Obsolete sample. The population clearly has not been shown or clearly cannot be assumed to be unchanged since the sample was taken, so it's clearly possible that the population has changed, making the generalization out of date. (Remember that 15 billion years isn't necessarily too old while an hour isn't necessarily recent enough.)

In 1843, 35% of all American families owned at least one buggy whip, that means that there's a 35% chance that there's a buggy whip in your house.

Considering that Americans almost completely stopped driving horse-drawn buggies once automobiles became widely available, information from when buggies were widely used is not going to represent present transportation related realities. (Key facts: Buggy whips are only needed by people who drive buggies, which are drawn by horses, and almost nobody uses horse-drawn transport nowadays.)

Dependent sample. The sampling method clearly has not been shown or clearly cannot be assumed to be random with respect to the feature being tested, so that it's clearly possible that the sample fails to accurately represent the population. (Remember that a "bias" that is not relevant to the feature being tested cannot be a problem.)

Did you know that they recently held a school assembly where they publicly interviewed 20 randomly chosen graduates of the schools Substance Control and Abuse Rejection Enterprise program, and 100% of those SCARE graduates reported that they've never tried drugs!

Considering that drugs are illegal, and that a student who publicly admits to having tried drugs is going to be in a lot of trouble, it wouldn't be surprising if some or all of those students were lying. (Key fact: people tend to give answers that please the questioners, especially if the questioners have power over them.)

This too counts as a counter argument. If my analysis turns out to be bad, then it's a bad counter argument. But it's still a counter argument, whether it's good or not.

Anecdotal Evidence. Here the arguer fixes on a particular story and tries to use it to support a generalization. The problem is that the anecdote could easily have been picked precisely because it supports the point the arguer wants to make, and might be screamingly atypical of the population he wants to generalize about.

Handgun Control, Inc. faked statistics on gun violence. That proves all gun-control activists are liars.

Key fact: That's just one incident, which could easily be the only such incident. No general survey is cited here.

That Mensa member tried to murder the people next door with thallium, and wrote snotty articles about it in the Mensa newsletter. That proves that all smart people are evil.

Key fact: That's just one incident, chosen because it's about a "smart" person attempting murder. There are thousands of other Mensa members and millions of other smart people.

Of course America was as deeply involved in witch burning as Europe was. Didn't you hear about the Salem Witch Trials?

Key fact: That's just one small series of incidents that might easily have been America's only literal witchhunt.

Keagan. Okay, I'll admit that some cops are racist. But you'll have to give me some pretty convincing evidence before I'll believe that all cops are racist.
Aylin. But didn't you see the Rodney King videotape? That videotape showed five white LAPD officers repeatedly beating a prone, unresisting black motorist. They just kept whaling on him, hitting him over and over again. It was a savage, stupid beating that King would not have gotten if he had been white. That proves all cops are racist thugs

It's true that Aylin gives a very salient example. That is, he gives an example that sticks out, or otherwise makes a deep impression on the listener. But salience isn't significance, and an example can be very salient without being at all representative.

Key Fact: This is exactly one incident that was chosen precisely because it supports the arguer's opinion, which makes it perfectly possibile that this was one of only a very few racist attacks by police officers.

By the way, did you notice that Keagan's argument relied on a claimed lack of evidence, and that Aylin's argument claimed to supply that evidence. This made Aylin's argument one of those rare cases of a direct argument that's also a counter argument. (Remember, this can only happens against an argument based on the claim that there's no evidence for something.

Begging the Question, or the Fallacy of Validation by Examples

I was once caught in a dispute with a person who obviously considered himself intelligent, educated and reasonable. At one point, this person made a sweeping and controversial generalization based on no evidence whatsoever. I asked him if he could back this up. His response was "let me validate with examples," by which he meant he was going to give me a series of cases each of which would be claimed to be an example of his thesis, and this was supposed to be logical evidence that he was right. Here is a (completely hypothetical) example of "validation by examples:"

Samantha. You know of course that the media has a conservative bias.
Lauren. Um, do you have some kind of survey or university study of randomly chosen news stories in which actual reporting was found to put a more positive spin on similar sets of facts when a conservative was involved than when a liberal was involved, because that's what you'd need to prove actual bias.
Samantha. Rubbish, you don't need that. I can validate this with examples. You remember when the media reported that liberal Democrat senator Gropemeister tended to get touchy with women who visited his office?
Lauren. Yeah, that was pretty creepy!
Samantha. Well the only reason they made such a big deal of it was because he was a liberal! If he'd been a conservative they'd have held back on front page stories describing the nasty details, the way they did when conservative Republican Mayor Longsuffering of Buffalo was caught doing the same thing.
Lauren. But didn't Longsuffering turn out to have been falsely accused by a mentally disturbed ex-employee? And he's only a medium city mayor, not a US senator, so...
Samantha. And I've got dozens of other examples. What about Representative Random and the . . .
Lauren. Oops! Look at the time. Gotta go.

If you look carefully at Samantha's arguments, you can see two distinct logical errors. The first is, of course, that she is "supporting" her claim with a set of anecdotes that she chooses herself rather than by properly collected and interpreted independent evidence. The second is that she's not just giving anecdotes, she's also adding in her own assumptions about what they mean. When she finds negative coverage of a liberal, she assumes that the negativity must be the result of bias, and likewise less negative coverage of a conservative must be a result of bias. Thus she builds her assumption of bias into her interpretations of her data, and thereby assumes the very thing she's supposed to prove.

The fallacy of begging the question consists of assuming something the arguer really needs to prove. Notice that each of Samantha's "examples" consists of her 1. alluding to a known incident (the Gropemeister incident) and 2. claiming, without a shred of evidence, that the way it was covered in the media (they made a big deal about it) was because of conservative bias. Thus Samantha does give some facts (the media made a big deal about Gropemeister) but the only thing that connects those facts to her conclusion is her assumption that the media has a conservative bias.

Red Herring

Apart from the fact that Red Herring is a very common fallacy, I mention it here because people often attack sampling arguments on the basis of sample age, sample size or sampling bias when these issues are completely irrelevant to the strength of the argument. Therefore, an arguer commits red herring if:

1. His criticism of a generalization is based on sample age when we have no reason to think that either the population or the sample has changed since the sample was taken.

2. His criticism of a generalization is based on sample size when we have no reason to think that this particular sample is too small for this particular population.

3. His criticism of a generalization is based on a bias in the sampling method when we have no reason to think that this particular bias has anything to do with the feature we're testing for.

Understanding Red Herring depends on understanding the concepts of "salience" and "relevance." A thing is salient when it is looks important to the issue. A thing is relevant when it actually is important. Salient things are not always relevant, and relevant things are not always salient. Something can look important when it really isn't, and seemingly unimportant details can sometimes be vital to understanding an issue. Red herring is committed whenever someone bases a conclusion on something that is salient (such as sample age, sample size or sampling method) but which in this particular instance is not relevant to the issue at hand.

Exercises

1. In your own words, write out the definition of "argument" used in this chapter.
2. What kind of statements are sampling arguments generally used to support?
3. In your own words, what are "generalizations?"
4. What do sampling arguments always start with?

Suppose that someone argues that 78% of all Irish people are Catholics because he has surveyed Irish hurling players, who make up 9% of the Irish people, and found out that 78% of Irish hurling players are Catholics.

5. What is the premise in this argument?
6. What is the conclusion in this argument?
7. What is the population in this example?
8. What is the sample in this example?
9. What is the feature in this example?
10. What is the fact (or evidence) in this example?
11. If we can't reasonably explain the fact without assuming the conclusion, what does that mean for this argument?
12. If we can reasonably explain the fact without assuming the conclusion, what does that mean for this argument?
13. Does the fact that a sample is very old necessarily mean that the argument is bad?
14. Does the fact that a sample is very small necessarily mean that the argument is bad?
15. Does the fact that a sample is not random necessarily mean that the argument is bad?
16. In your own words, what is "population structure?"
17. In your own words, what is the first thing you think about when you consider sample size?
18. In your own words, what is the second thing you think about when you consider sample size?
19. In your own words, what is the first thing you think about when you consider sample age?
20. In your own words, what is the second thing you think about when you consider sample age?
21. In your own words, what is the first thing to think about when you consider the randomness or nonrandomness of a sample?
22. In your own words, what is the second thing to think about when you consider the randomness or nonrandomness of a sample?
23. In your own words, what is a "key fact?"
24. In your own words, define "inadequate sample."
25. In your own words, define "obsolete sample."
26. In your own words, define "dependent sample."
27. In your own words, define "anecdotal evidence."
28. In your own words, define "red herring."
29. What is "salience?"
30. What is "relevance?"
31. In your own words, define "begging the question."
32. In your own words, define "validation by examples."
33. How is "validation by examples" related to the other fallacies in this chapter?
34. What are the three different ways an arguer can commit red herring in criticizing sampling arguments?

Answers

1. An "argument" is an attempt to persuade someone to believe something.
2. Sampling arguments are generally used to support generalizations.
3. "Generalizations" are general statements that make claims about all of some certain kind of thing.
4. Sampling arguments always start with a sample taken from some larger population.
5. The premise is "78% of Irish hurling players are Catholics."
6. The conclusion is "78% of all Irish people are Catholics."
7. The population is Irish people.
8. The sample is Irish hurling players.
9. The feature is the proportion of Catholics.
10. The fact is "78% of Irish hurling players are Catholics." (This time it's the same as the premise.)
11. If we can't reasonably explain the fact without assuming the conclusion, that means the argument is good.
12. If we can reasonably explain the fact without assuming the conclusion, that means the argument is not good.
13. A sample being very old does not necessarily mean that the argument is bad.
14. A sample being very small does not necessarily mean that the argument is bad.
15. A sample not being random does not necessarily mean that the argument is bad.
16. "Population structure" is the way different parts of a population are arranged relative to each other.
17. How large is the sample compared to the number of different relevant properties individuals in the population can have?
18. How is the population structured?
19. How quickly and in what ways do the things in this population and sample change over time?
20. Given this rate of change, do we have a reasonable guarantee that the sample is still representative of the population?
21. What are all the characteristics of particular fraction of the population picked out by this method?
22. How are the characteristics of this fraction related to the feature of the sampling argument?
23. A "key fact" is something about an argument that makes it a good or bad argument.
24. "Inadequate sample" is when a population is too unevenly structured to be represented by the given sample size.
25. "Obsolete sample" is when a population is changes too rapidly to be represented by a sample of the given age.
26. "Dependent sample" is when the sampling method is somehow related to the feature.
27. "Anecdotal evidence" is when people talk about a few selected cases rather than giving a properly conducted sample.
28. "Red herring" is when someone talks about something that is salient but not relevant.
29. "Salience" is when something sticks out and looks important, even though it might not mean anything.
30. "Relevance" is when something actually matters, even if it doesn't immediately seem important.
31. "Begging the question" is when someone assumes something they actually need to prove.
32. "Validation by examples" is when someone gives a set of anecdotes and just assumes that they support his point.
33. "Validation by examples" is a combination of begging the question and anecdotal evidence.
34. An arguer can commit red herring by saying a sample is too old when it isn't, saying a sample is too small when it isn't, or saying a sample is too nonrandom when that doesn't matter.

Copyright � 2013 by Martin C. Young

This Site is Proudly Hosted By.