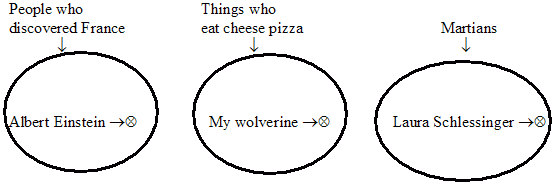
| Paris is in France Berlin is in Germany Compton is in America |
Cats are mammals Dogs are mammals Ferrets are mammals |
People have two legs Mammals have four legs Insects have six legs |
Dumbledore is a wizard Gandalf is a wizard Merlin is a wizard |
| Albert Einstein discovered France My wolverine eats cheese pizza Laura Schlessinger is a Martian |
Fa Pw Ml |
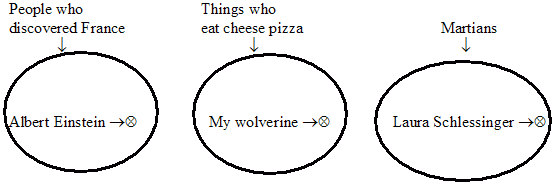
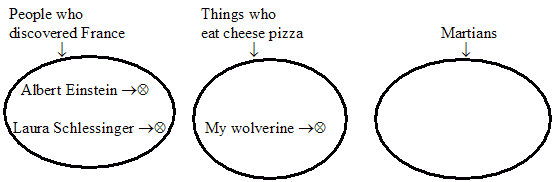
| Elvis is dead. (Accept it.) The X-Files was a popular TV show The Eiffel Tower is in France |
De Px Ft |
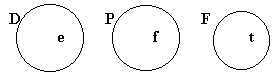
| An argument with premises that can't all be true IS necessarily valid. |
Elvis is dead. Elvis is alive. Laura Schlessinger is a woolly mammoth. |
De ~De Wl VALID!! |
| Homework 3. Answer the following questions either on your own paper or on the Homework 3 Answer Sheet 1. Circle the valid arguments. Cross out the invalid arguments A. If the British had caught and executed Benjamin Franklin in 1777, Benjamin Franklin would be dead. Benjamin Franklin is not dead, so the British did not execute Benjamin Franklin. B. If the British had caught and executed Benjamin Franklin in 1777, Benjamin Franklin would be dead. The British did not execute Benjamin Franklin, so Benjamin Franklin is not dead. C. If the British had caught and executed Benjamin Franklin in 1777, Benjamin Franklin would be dead. The British did execute Benjamin Franklin, so Benjamin Franklin is dead. D. If the British had caught and executed Benjamin Franklin in 1777, Benjamin Franklin would be dead. Benjamin Franklin is dead, so the British did execute Benjamin Franklin. 2. Circle the valid arguments. Cross out the invalid arguments A. Whales are fish. Whales are not fish. So cheese is a mineral. B. Whales are mammals. Whales are not fish. So cheese is not a mineral. C. Whales are mammals. Whales are fish. Fish are never mammals. So whales are fish. D. Whales are mammals. Fish are never mammals. Whales are not fish. So some whales eat fish. 3. Circle the deductive arguments. Cross out the inductive ones. A. All whales are fish. Willie is a whale. Therefore Willie is a fish. B. The vast majority of whales live free in the ocean. Willie is a whale. Therefore Willie lives free in the ocean. C. All monkeys can fly. George cannot fly. Therefore George is not a monkey. D. Monkey aerodynamics make flight extremely unlikely. Kong is a monkey. Therefore Kong cannot fly. |
